Delayma-Models

Delayma: A Comprehensive Approach to Accurate Flight Delay Forecasting

Authors:

Table of Contents

Motivation

Flight delays have long been a centre of uncertainty in the aviation industry, having widespread effects on the aviation industry and passengers. It is a critical concern within the aviation industry, impacting passenger satisfaction, operational costs, and overall system efficiency. Prediction of delay can have far-reaching consequences on the entire industry and is of huge economic importance.

Accurately predicting flight delays is a crucial point of research as it is affected by various factors such as weather, air traffic congestion, logistic complexities, festivities, and economics. Developing reliable prediction models can revolutionize how airlines manage their schedules and how passengers plan their journeys. This study aimed to create a modern ML model which can accurately predict delays based on- season, time, location, etc. For this study, we used various datasets and intend to employ relevant ML algorithms to correctly predict delays, coupled with relevant visualization analysis and data engineering techniques.

Several attempts have been made before to predict flight delays.

Dataset Details

The dataset source is taken from a kaggle dataset, which contains information about flights that took off from JFK Airport between November 2019 and January 2020.

Insights from the dataset

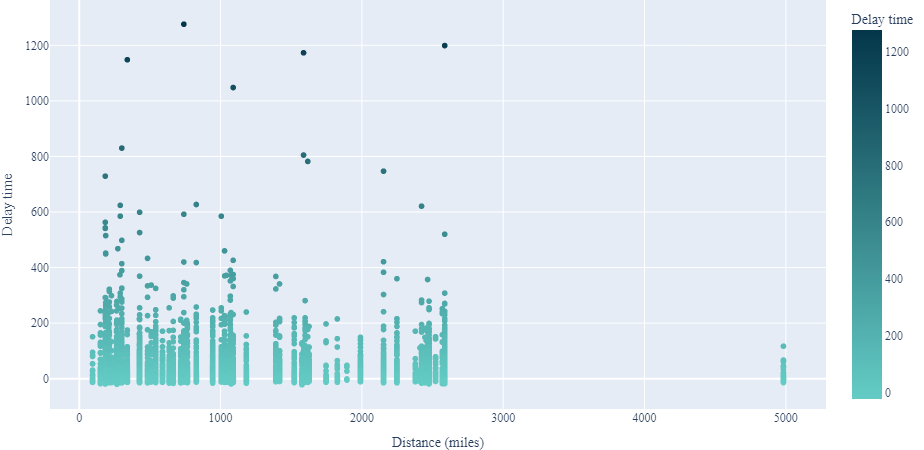
delay_vs_dist

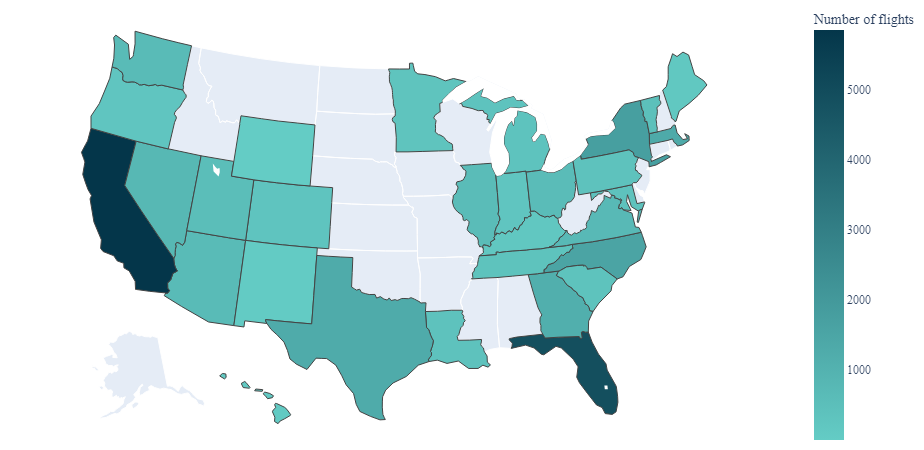
dest_states

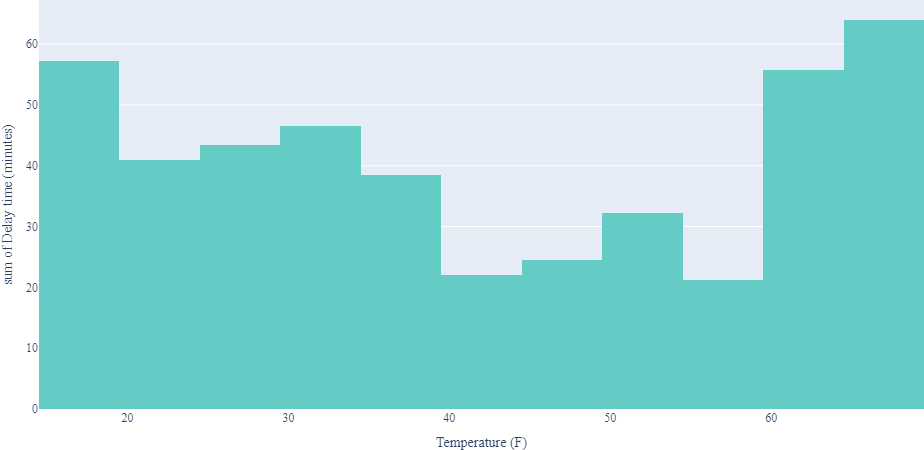
temp_vs_delay

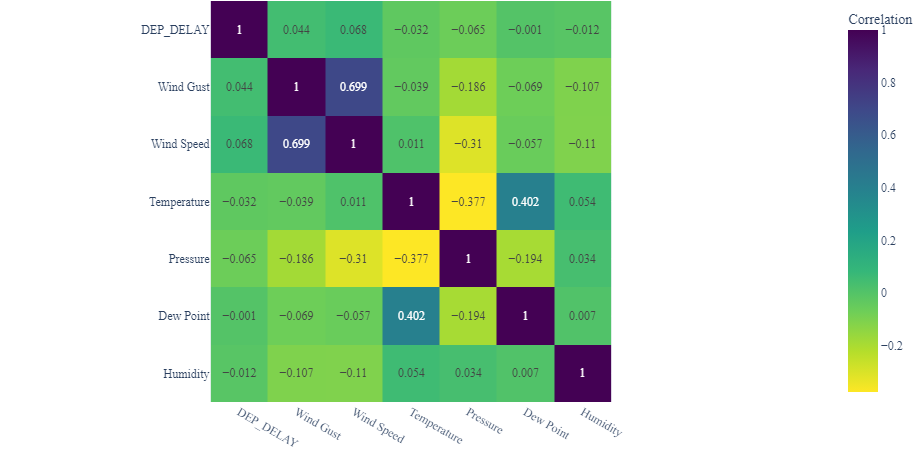
weather_corr

How we used the dataset

The DEP_DELAY column in the datasets used for Classification was transformed into binary classes. A flight was marked as delayed if the departure time was more than 15 minutes later than scheduled.

To make the classification task more manageable, we started with a smaller subset of the problem before expanding to the larger one. To proceed, four sub-datasets were created from this.

In the context of the regression problem, the DEP_DELAY column was utilized in its original form.

Data Pre-processing

Basic preprocessing, which was done on the complete dataset:

  1. The Condition attribute originally contained 25 unique conditions. Some data entries had multiple conditions listed in the Condition field. We first carried out an encoding process akin to label encoding but in a monotonically increasing manner. For instance, various types of cloudiness, like mostly cloudy and partly cloudy were assigned the numbers 2 and 1, respectively. Each condition was allocated its column, leading to the creation of 9 additional columns and the removal of the original Condition column.

  2. Attributes such as day, month, hour, and minute exhibit cyclical behaviour. We employ a technique known as cyclic feature engineering to capture this periodicity. This method involves mapping each cyclical attribute onto a circle, ensuring the preservation of its periodic characteristics. As a result, we applied cyclic feature engineering to the MONTH, DAY_OF_WEEK, and DAY_OF_MONTH columns.

We initially tackled a less complex subset of the problem to streamline the problem-solving process. This approach allowed us to scale up our efforts gradually. Consequently, we partitioned the original dataset into four distinct, manageable sub-datasets.

Datasets used for Classification had their DEP_DELAY column converted to binary classes based on delay, where delay is true if the departure time delay exceeds 15 minutes.

Feature Format Description
MONTH int64 month
DAY_OF_MONTH int64 date on which flight departed
DAY_OF_WEEK int64 day number of the week on which flight departed
OP_UNIQUE_CARRIER object Carrier Code
TAIL_NUM object Airflight Number
DEST object Destination
DEP_DELAY float64 Departure delay of the flight
CRS_ELAPSED_TIME int64 Scheduled journey time of the flight
DISTANCE int64 Distance of the flight
CRS_DEP_M int64 Scheduled Departure Time
CRS_ARR_M int64 Scheduled Arrival Time
Temperature int64 Temperature
Dew Point object Dew Point
Humidity int64 Humidity
Wind object Wind type
Wind Speed int64 Wind speed
Wind Gust int64 Wind Gust
Pressure float64 Pressure
Condition object Condition of the climate
sch_dep int64 No. of flights scheduled for arrival
sch_arr int64 No. of flights scheduled for departure
TAXI_OUT int64 Taxi-out time
Cloudy int64 Cloudy intensity
Windy int64 Windy intensity
Fair int64 Fair intensity
Rain int64 Rain intensity
Fog int64 Fog intensity
Drizzle int64 Drizzle intensity
Snow int64 Snow intensity
Wintry Mix int64 Wintry Mix intensity
Freezing Rain int64 Freezing Rain intensity
MONTH_sin float64 Sin value of month
MONTH_cos float64 Cos value of month
DAY_OF_MONTH_sin float64 Sin value of day of month
DAY_OF_MONTH_cos float64 Cos value of day of month
DAY_OF_WEEK_sin float64 Sin value of day of the week
DAY_OF_WEEK_cos float64 Cos value of day of the week

The attributes MONTH, DAY_OF_MONTH, and DAY_OF_WEEK underwent a transformation into sine and cosine values to encapsulate their cyclical nature. The attributes Temperature, Dew Point, Wind, and Condition were converted into numerical representations. As part of the preprocessing phase, new columns such as Cloudy, Windy, Fair, Rain, Fog, Drizzle, Snow, Wintry Mix, and Freezing Rain were introduced into the dataset. Subsequently, the original columns MONTH, DAY_OF_MONTH, DAY_OF_WEEK, and Condition were removed from the dataset.

Methodology

Baseline for classification

We have successfully replicated the results from previous studies, utilizing the same algorithms to establish a baseline. To address the significant class imbalance in our preprocessed data, we employed the Synthetic Minority Oversampling Technique (SMOTE). This technique leverages the KNN algorithm to synthesize samples from minority classes. After mitigating the class imbalance, we partitioned the data into an 80:20 split and performed scaling. Subsequently, we used the Boruta algorithm, a sophisticated feature selection method with Random Forests, to select the most relevant features. The Random Forest model yielded the highest scores, as detailed below:

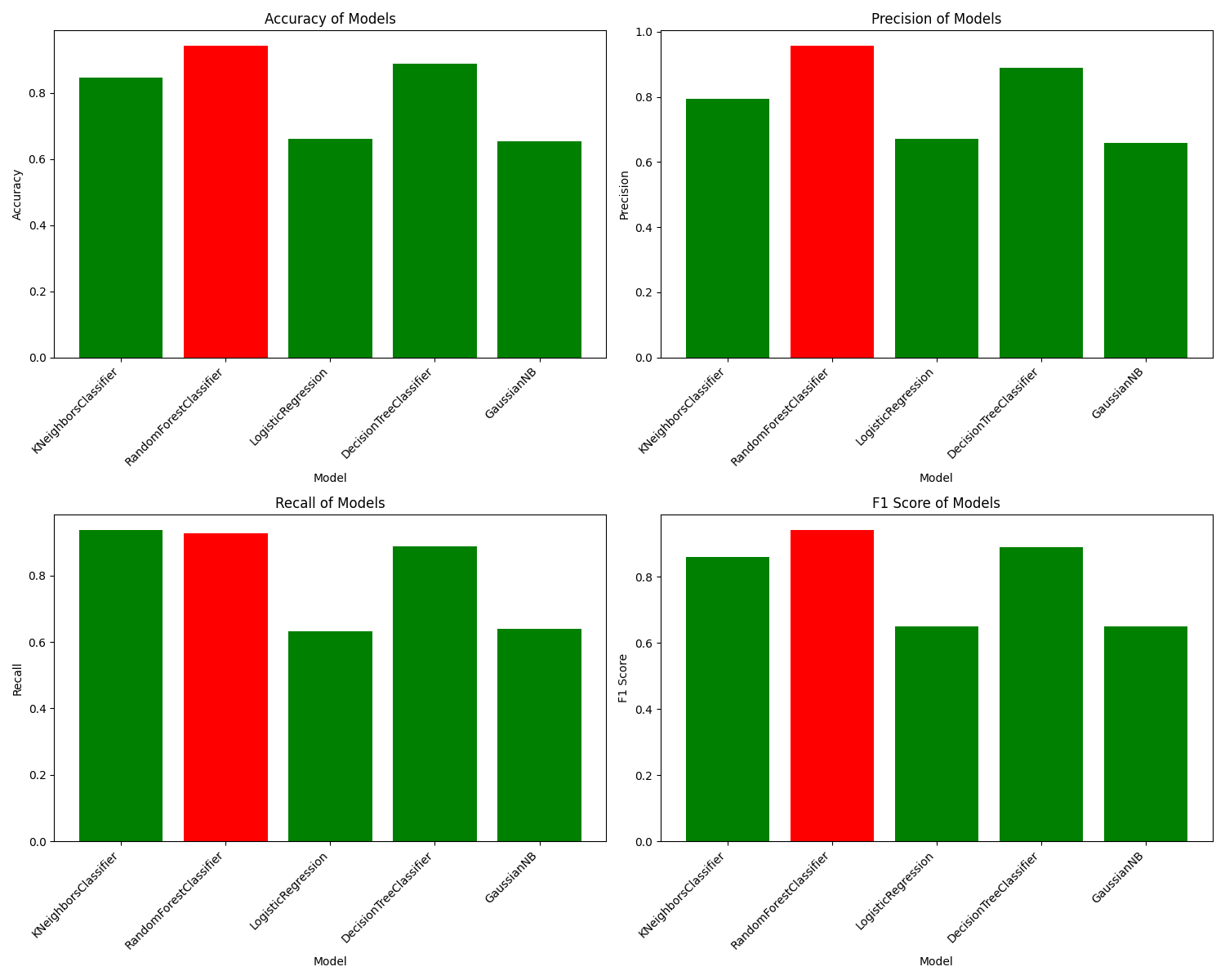
Baseline Results

Classification

We used multiple algorithms for multiple datasets and compared their performance.

Dataset Algorithm Hyperparameters
df_1_3 Logistic Regression Penalty = l2, Tolerance = 10-5, Max Iterations = 500, Solver = lbfgs
  Bayesian Classifier Alpha = 0.1
  Passive Aggressive Classifier Default
  SGD Classifier Default
df_1_10 Logistic Regression C = 0.01, max_iter = 103
  Random Forest Classifier max_depth = 4, max_features = ‘log2’, n_estimators = 100
df_1_25 Random Forest Classifier n_estimators = 400
  XGBoost Classifier colsample_bytree = 1.0, gamma = 0, max_depth = 5, min_child_weight = 5, subsample = 1
  LightGBM Classifier num_leaves = 102
  CatBoost Classifier depth = 5, iterations = 103, learning_rate = 0.1

The models were evaluated using key metrics such as Accuracy, Precision, Recall, and F1-Score.

Regression

After getting more than 97% accuracy in classification, we moved on to regression. We did a regression on the entire dataset.

We initially used the following algorithms and did hyperparameter tuning on them without removing outliers:

Model Hyperparameters MSE Standard Deviation R2 Score
RandomForestRegressor max_depth=5, n_estimators=10, random_state=1 8.181 40.707 0.995
PolynomialFeatures   1.348 x 10-19 41.943 1.0
Ridge alpha=0.1 1.701 x 10-14 41.943 1.0
Lasso alpha=0.1 1.015 x 10-5 41.940 1.0
BayesianRidge   1.472 x 10-24 41.943 1.0
ElasticNet alpha=0.1 9.800 x 10-6 41.940 1.0

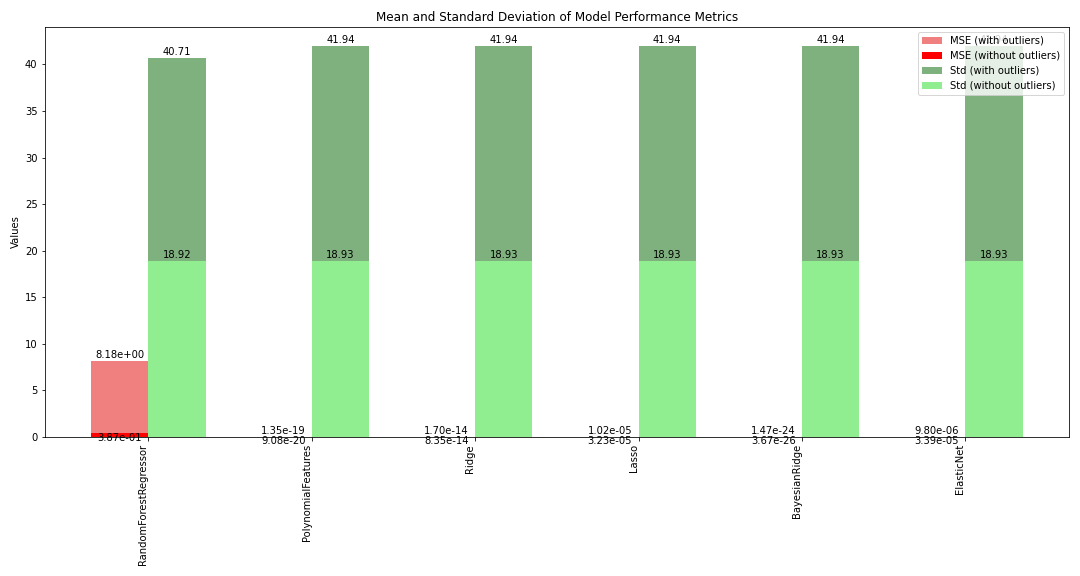
Our model yields a low Mean Squared Error (MSE) and a high R2 score, which are positive indicators. However, the high standard deviation suggests the presence of outliers in our dataset. To address this, we employed the z-score method with a threshold of 3.0 to identify and remove these outliers. The results post-outlier removal are as follows:

Model Hyperparameters MSE Standard Deviation R2 Score
RandomForestRegressor max_depth=5, n_estimators=10, random_state=1 0.387 18.923 0.999
PolynomialFeatures   9.078 x 10-20 18.932 1.0
Ridge alpha=0.1 8.345 x 10-14 18.932 1.0
Lasso alpha=0.1 3.235 x 10-5 18.926 1.0
BayesianRidge   3.670 x 10-26 18.932 1.0
ElasticNet alpha=0.1 3.387 x 10-5 18.926 1.0

The results reveal a substantial reduction in the standard deviation, except for Logistic Regression. This is primarily because Logistic Regression is not ideally suited for regression tasks. Furthermore, a notable decrease in the Mean Squared Error (MSE) indicates improved model performance. The R2 score has also significantly increased, nearing the optimal value 1.0. This improvement can be attributed to the removal of outliers that were previously skewing the R2 score. Overall, these results suggest that our model is performing exceptionally well.

Results

The results using multiple algorithms for multiple datasets are as follows:


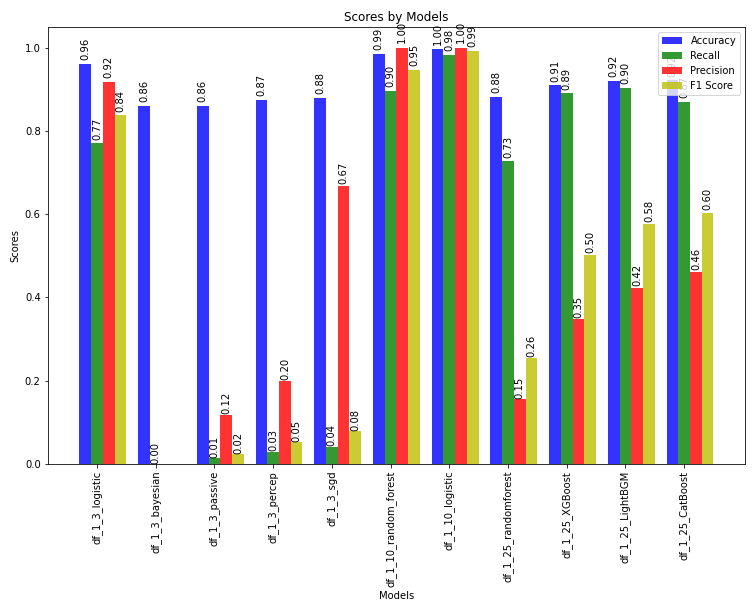
Classification Results


Logistic regression seemed to be a consistent model throughout all the different datasets, achieving almost 100% accuracy.

We trained the model on a complete train set using these algorithms with the same hyperparameters as were used in the other datasets and got the following results:

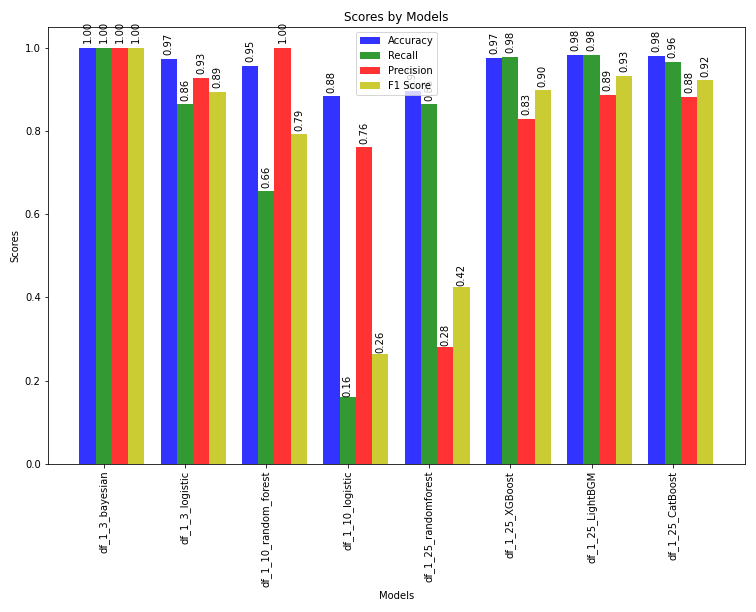
Classification Results

The labels in the graph above represent which model was used to train the complete train set.

Here is the comparison of the results of the algorithms with default parameters on the complete train set before and after removing outliers:


Classification Results


Conclusion and Future Work

Our findings suggest that we have successfully fine-tuned a Bayesian Ridge Regression model to predict flight delays accurately. This model can be utilized to anticipate delays and implement preventative measures. While the model has performed well on our dataset, testing it on larger, real-time datasets would be more complex and challenging. Real-time data often contains incomplete information, resulting in numerous empty fields that must be handled. Despite these challenges, the potential benefits are significant. For instance, these predictive models could notify passengers about delays in advance, allowing them to adjust their travel plans accordingly.

References

  1. Yi et al., Link to Paper ↩

  2. Esmaeilzadeh and Mokhtarimousavi, Link to Paper ↩

  3. Zhang and Ma, Link to Paper ↩

  4. Tang, Link to Paper ↩

This site is open source. Improve this page.